udacity_highway05
Udacity中坐标转换
汽车自动驾驶三个坐标系
笛卡尔坐标系,Frenet坐标系,汽车自身的坐标系
cartesian_to_frenet 笛卡尔坐标转 Frenet坐标
1 | cartesian_to_frenet(double x, double y, double theta, std::vector<double> maps_x, std::vector<double> maps_y) |
笛卡尔坐标就是正常的(x,y)坐标系,Frenet坐标使用的是(s,d)s是沿着道路行进的距离,也可以称作纵向距离,d 是横向距离,称作道路法向的距离。
在Udacity中将笛卡尔转到Frenet 步骤:
首先获取(x,y)的下一个地图点(next_x,next_y),从地图信息中。
方法,遍历地图信息,计算distance, 找到距离这个点最小的 point. (next x,next y)
这个点的前一个点就为(prev_x,prev_y)
以(prev_x,prev_y)作为原点,计算得到新的坐标(next_x,next_y)变成(n_x,n_y),(x,y)变成(x_x,x_y)
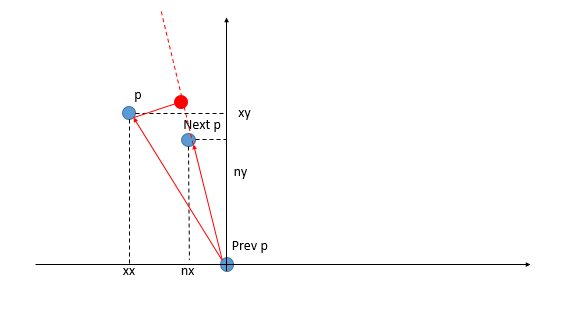
做一个映射,得到点(x,y)在线段(nx,ny)和(px,py),上的点(proj_x,proj_y),计算两点之间的距离,得到的是 d,但是要判断d的正负,就需要借助中心点,计算中心点距离两个点的距离1
2
3
4double center_x = 1000 - maps_x[prev_wp];
double center_y = 2000 - maps_y[prev_wp];
double centerToPos = distance(center_x, center_y, x_x, x_y);
double centerToRef = distance(center_x, center_y, proj_x, proj_y);
通过距离来判断是否和中心点处在同一侧1
2if (centerToPos <= centerToRef)
frenet_d *= -1;
计算s
从地图的第一个点开始加s,一直加到prev_p,然后计算 投影的点到新坐标的原点的距离1
2
3
4for (int i = 0; i < prev_wp; i++)
frenet_s += distance(maps_x[i], maps_y[i], maps_x[i + 1], maps_y[i + 1]);
frenet_s += distance(0, 0, proj_x, proj_y);
得到 Frenet S
frenet_to_cartesian Frenet坐标 转 笛卡尔坐标
1 | frenet_to_cartesian(double s, double d, std::vector<double> maps_s, std::vector<double> maps_x, std::vector<double> maps_y) |
因为地图中两个格式的坐标系坐标都有
所有 根据输入的s,先找到距离最近的地图点(prev_wp)
找到第二近的点就为 wp2 = (prev_wp + 1)% maps_x.size(); 这个是点的序列号
double heading = atan2((maps_y[wp2] - maps_y[prev_wp]), (maps_x[wp2] - maps_x[prev_wp]));
之后找出这两个点之间的斜率。这里使用atan2返回的是有方向的-pi~pi之间的大小
再找到s距离最近点之间的线段距离1
double seg_s = (s - maps_s[prev_wp]);
有了线段的距离,线段的斜率,就可以转化成线段的x和y.1
2double seg_x = maps_x[prev_wp] + seg_s*cos(heading);
double seg_y = maps_y[prev_wp] + seg_s*sin(heading);
但是还没有加上偏移的d分量,所以接下来计算偏移量
先获取一个夹角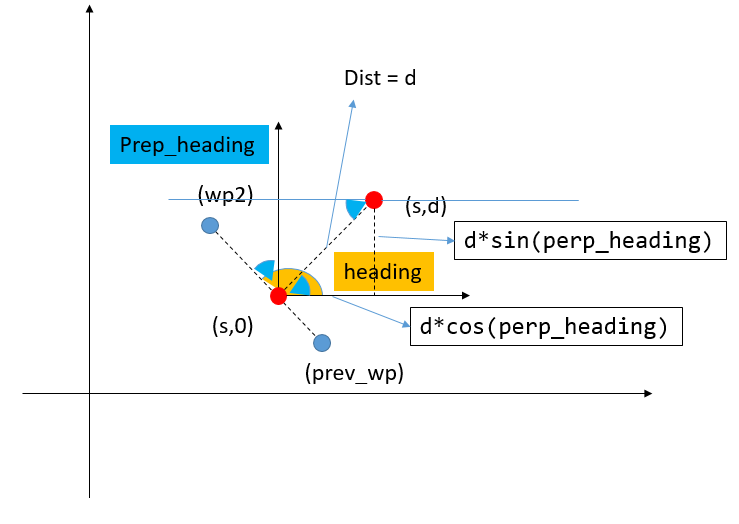
1
double perp_heading = heading - pi / 2;
再进行叠加1
2double x = seg_x + d*cos(perp_heading);
double y = seg_y + d*sin(perp_heading);
最后返回{x,y}
return { x,y };
笛卡尔坐标 转汽车自身坐标 笛卡尔坐标
旋转到汽车参考系,可以让计算变的简单一点
这里车体坐标系,车头朝向是Y,右侧是X,这里如果改成纵向和横向,会更好
所要做的只是减去汽车的坐标
1 | double shift_x = pts_x[i] - ref_x; |
这里使用0-ref_yaw因为x1坐标系与x0坐标系旋转的角度是负的,顺时针旋转了。


