MPC介绍

在工程技术方面，MPC全称可指Model Predictive Control模型预测控制（又称RHC, Receding Horizon ）。MPC指一类算法，周期性基于当帧测量信息在线求解一个有限时间开环优化问题，并将结果的前部分控制序列作为被控对象。根据所用模型不同，分为动态矩阵控制（DMC），模型算法控制（MAC）、广义预测控制（GPC）。在智能驾驶方向，重点在于基于状态空间模型的模型预测控制。

初识模型预测控制

https://www.bilibili.com/video/BV1pV411n7uN
这个B站教学视频堪称经典，投币点赞加收藏。找原著作者Ally寻到了这份教案。感谢原作者Ally。教案原件就不分享了，这里手敲教案，分享一下。

根据高中物理知识，将篮球视为质点，在不考虑空气阻力作用下，设篮球斜抛的角度为θ，斜抛初始速度为v，初始高度为y0（右图为0），则篮球的斜抛运动由竖直方向的上抛运动和水平方向的匀速运动构成：

（1）竖直方向：

$$y(t)=y_{0}+v \sin \theta \cdot t-\frac{1}{2} g t^{2}$$

（2）水平方向

$$x(t)=v \cos \theta \cdot t$$

那么对于离初始点水平距离为l、竖直距离h的球框位置，若想在初始投球点能够顺利投中球框位置，可以联立上面两式求得一组解集（v, θ ）。

式子1 和式子2 就是模型，篮球能否按照预期投进框里，就是预测，通过调整初始点投球的角度和速度就是控制。
在这里不考虑空气阻力等因素。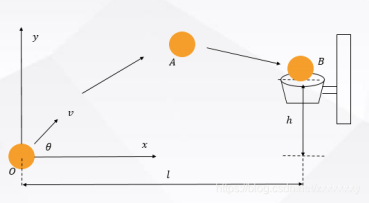

模型

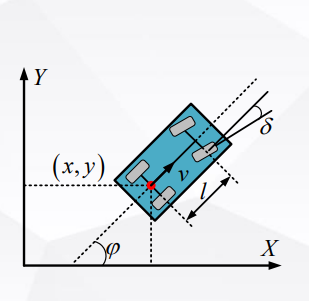
设车辆的状态量偏差和控制量偏差如式 (3) 所示：

$$\tilde{\boldsymbol{x}}=\left[\begin{array}{c} \dot{x}-\dot{x}_{r} \\ \dot{y}-\dot{y}_{r} \\ \dot{\varphi}-\dot{\varphi}_{r} \end{array}\right], \tilde{\boldsymbol{u}}=\left[\begin{array}{c} v-v_{r} \\ \delta-\delta_{r} \end{array}\right]$$

基于第9讲的运动学模型的离散状态空间方程如下，

$$\tilde{x}(k+1)=\left[\begin{array}{ccc} 1 & 0 & -T v_{r} \sin \varphi_{r} \\ 0 & 1 & T v_{r} \cos \varphi_{r} \\ 0 & 0 & 1 \end{array}\right] \tilde{x}(k)+\left[\begin{array}{cc} T \cos \varphi_{r} & 0 \\ T \sin \varphi_{r} & 0 \\ T \frac{\tan \varphi_{r}}{l} & T \frac{v_{r}}{l \cos ^{2} \delta_{r}} \end{array}\right] \tilde{u}(k)=a \tilde{x}(k)+b \tilde{u}(k)$$

定义输出方程：

$$\boldsymbol{y}(k)=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \tilde{\boldsymbol{x}}(k)=\boldsymbol{c} \tilde{x}(k)$$

构建新的状态向量：

$$\boldsymbol{\xi}(k)=\left[\begin{array}{c} \tilde{x}(k) \\ \tilde{u}(k-1) \end{array}\right]$$

那么新的状态空间表达式：
$\boldsymbol{\xi}({k+1})=\left[\begin{array}{c}\tilde{x}(k+1) \\ \tilde{u}(k)\end{array}\right]=\left[\begin{array}{c}a \tilde{x}(k)+b \tilde{u}(k) \\ \tilde{u}(k)\end{array}\right]=\left[\begin{array}{c}\tilde{x}(k)+b \tilde{u}(k-1)+b \tilde{u}(k)-b \tilde{u}(k-1) \\ \tilde{u}(k-1)+\tilde{u}(k)-\tilde{u}(k-1)\end{array}\right]=\left[\begin{array}{c}a \tilde{x}(k)+b \tilde{u}(k-1) \\ \tilde{u}(k-1)\end{array}\right]+\left[\begin{array}{c}b \tilde{u}(k)-b \tilde{u}(k-1) \\ \tilde{u}(k)-\tilde{u}(k-1)\end{array}\right]$
$=A \boldsymbol{\xi}(k)+\boldsymbol{B} \Delta \tilde{\boldsymbol{u}}(k)$
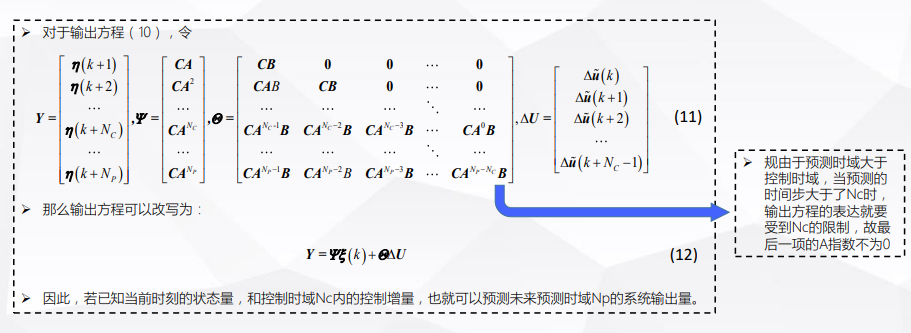
那么输出方程为 :

$$\boldsymbol{\eta}(k)=\left[\begin{array}{ll} \boldsymbol{I}_{N_{x}} & \boldsymbol{0} \end{array}\right]\left[\begin{array}{c} \tilde{\boldsymbol{x}}(k) \\ \tilde{\boldsymbol{u}}(k-1) \end{array}\right]=\boldsymbol{C} \boldsymbol{\xi}(k)$$

预测

这里公式太复杂了，，直接贴图吧。

https://www.bilibili.com/video/BV1pV411n7uN

$$\begin{aligned} &\min _{\Delta U} J=\frac{1}{2} \Delta \boldsymbol{U}^{\mathrm{T}} \boldsymbol{H} \Delta \boldsymbol{U}+\boldsymbol{g}^{\mathrm{T}} \Delta \boldsymbol{U} \\ &\text { s.t. }\left\{\begin{array}{c} \boldsymbol{A}_{t} \Delta \boldsymbol{U}_{t} \leq \boldsymbol{U}_{\max }-\boldsymbol{U} \\ \boldsymbol{A}_{l} \Delta \boldsymbol{U}_{t} \leq-\boldsymbol{U}_{\mathrm{nin}}+\boldsymbol{U}_{t} \\ \Delta \boldsymbol{U}_{\min } \leq \Delta \boldsymbol{U} \leq \Delta \boldsymbol{U}_{\mathrm{max}} \end{array}\right. \end{aligned}$$

这个是不是和LQR很像！！
之后会更一个MPC做的项目，敬请期待！

g感谢参考

https://www.jianshu.com/p/036a31bb62b5
https://baike.baidu.com/item/%E6%A8%A1%E5%9E%8B%E9%A2%84%E6%B5%8B%E6%8E%A7%E5%88%B6
https://www.guyuehome.com/33800
https://www.bilibili.com/video/BV1pV411n7uN