torch.bmm 介绍

很多框架中提供的矩阵乘法都是出于简化计算的考虑，很多情况下在进行计算时候都会牵扯到 batch size 这一个维度，这就使得很多矩阵的计算是三维的，Pytorch中的bmm()函数就可以很方便的实现三维数组的乘法，而不用拆成二维数组使用for循环解决。

看程序遇到好多torch的方法，一一记录。

torch.bmm() 函数定义

def bmm(self: Tensor,
        mat2: Tensor,
        *,
        out: Optional[Tensor] = None) -> Tensor

函数的传入参数很简单，两个三维矩阵而已，只是要注意这两个矩阵的shape有一些要求：

res = torch.bmm(ma, mb)
ma: [a, b, c]
mb: [a, c, d]

也就是说两个tensor的第一维是相等的，然后第一个数组的第三维和第二个数组的第二维度要求一样，对于剩下的则不做要求，其实这里的意思已经很明白了，两个三维矩阵的乘法其实就是保持第一维度不变，每次相当于一个切片做二维矩阵的乘法。

就像，第一次从ma的a个里面取出一个矩阵，矩阵维度是（b x c）。
从mb的b个里面取出一个矩阵，矩阵维度是（c x d）。 这样两个矩阵就能形成相乘，得出的结果是 （b x d）。最后将会得到a 个 （b x d），最后就会组成一个[a,b,d]的三维矩阵。

下面看图解

先定义tensor

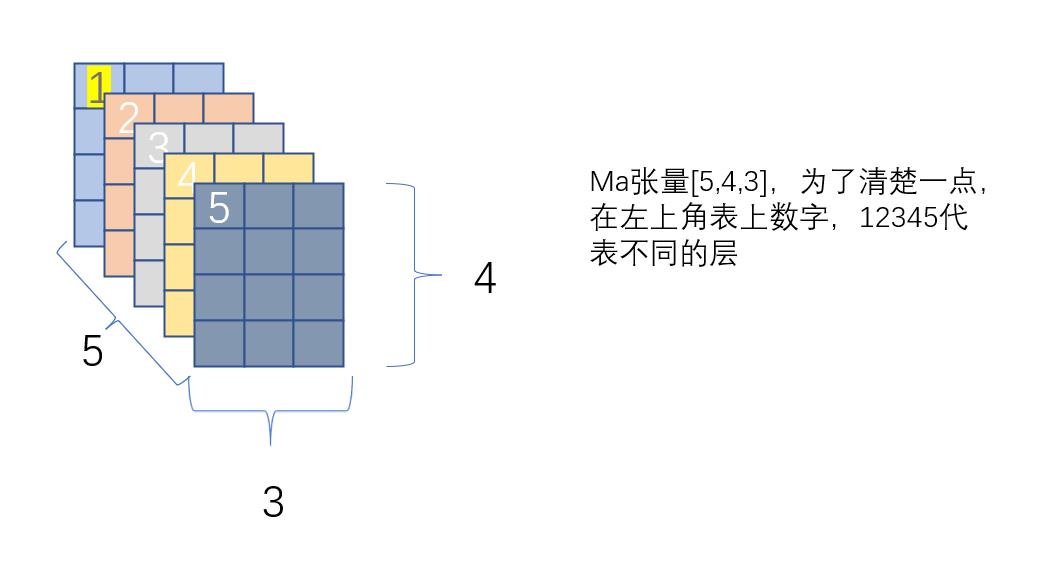
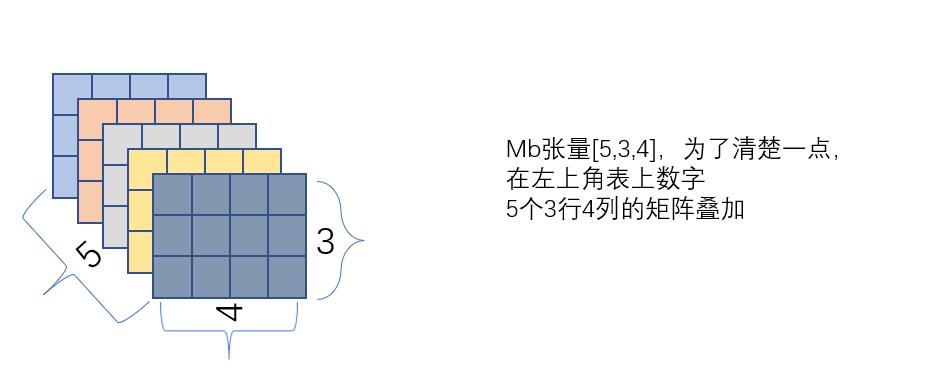
开始计算

从两个tensor中，取出第一层，开始进行计算，相乘。
即，看图，从两个tensor中均去除第一层，淡蓝色部分，之后进行矩阵的乘法，得（4x3）*（3x4）=(4x4)。即4行3列的矩阵A乘以，3行4列的矩阵B,可以得到4行4列的矩阵C。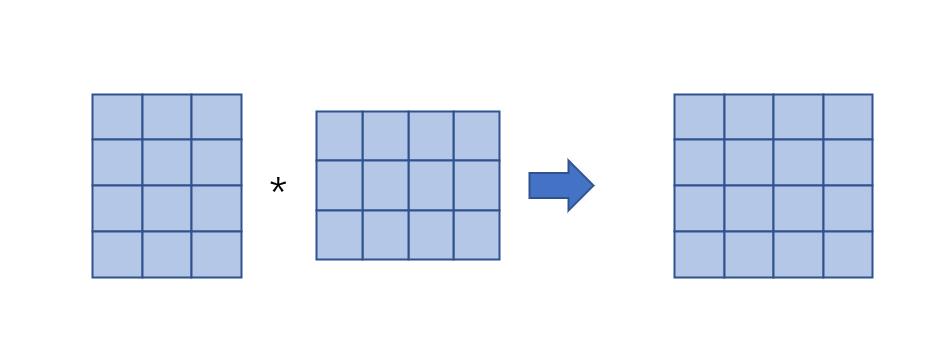

之后将其至于一个新的tensor的第一层，重复进心5次计算，即可得到一个新的tensor,[5,4,4]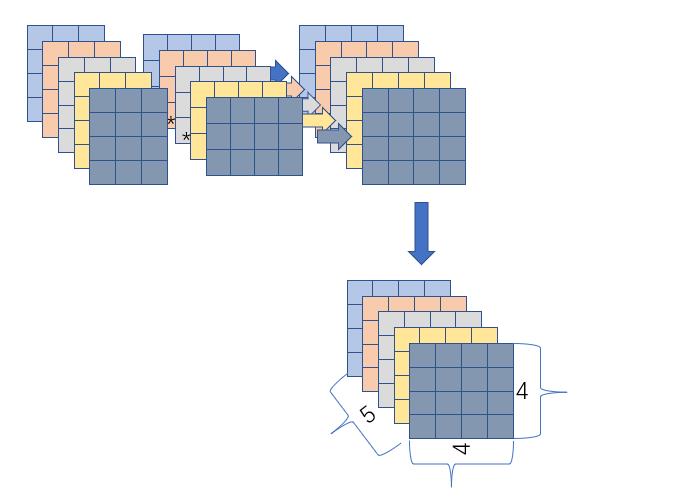

整体图片解释