介绍
The D_star Lite algorithm is a path planning algorithm proposed by Koenig S and Likhachev M based on the LPA_star algorithm.
LPA_star 算法还是A_star 算法都不能满足移动机器人在未知环境中的路径规划需求
D_star 算法虽然可以实现未知环境的路径规划,但效率较低
When the mobile robot proceeds along the planned path, the node it reaches is set as the starting node. Therefore, when the path changes or the key value needs to be updated, the heuristic value and estimated cost from the target node to the new node need to be updated. As the mobile robot keeps approaching the target node, the heuristic value of the node will continue to decrease, and it will not exceed h (start Org, start New). Since the same value must be subtracted each time, the order of opening the list will not change, so this part of the calculation may not be performed, thus avoiding the queue traversal process every time the path changes.
在移动机器人按照规划的路径进行前进时其所到的节点即设置为起始节点,因此路径变化或者key值需要更新时,需要更新从目标点到新起点的启发值以及估计成本。由于移动机器人不断的靠近目标点,节点的启发值将不断减少,且减少至不会超过h(start Org,start New)。由于每次都要减去相同的值,开启列表的顺序并不会改变,因此可以不进行这部分的计算,这样便避免了每次路径改变时的队列遍历过程。
If an obstacle is found during the forward process, set the location of the environment map corresponding to the obstacle as the obstacle space, and use it as the starting node to re-plan a path using the “path field” information.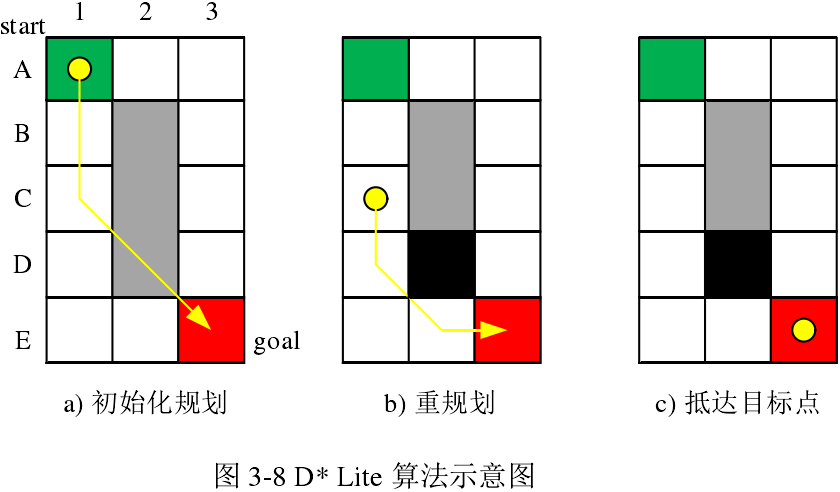
definition
- g*(s) Record the predecessor node of the grid node
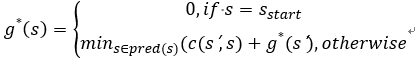
- rhs(s) records the g(s) of the successor node of the grid node, and has the formula:
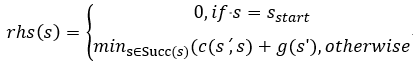
- When evaluating the estimated value of grid points, D_star Lite also introduces the value of k(s) for comparison, where k(s) contains two values [k(s1); k(s2)], which respectively satisfy the following formulas:
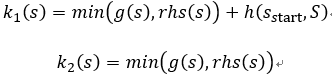
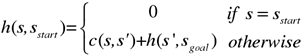
Example
When the map has not changed
To explain the workflow of the algorithm with a specific example:
First, calculate the heuristic value h from the starting node B1 → the target point E3 as shown in the figure above. The value of h approximates the maximum value of the absolute difference between the x and y coordinates of the two grids from the starting grid to the current grid. The specific process of the D*Lite algorithm is shown in the figure below.
In the Initialization phase, set g=rhs=∞ in all feasible nodes.
In the first step, step1, the nodes around E3, D2, E2, and D3, are calculated. Taking D3 as an example, calculate rhs(s)=min(g(s’)+c(s,s’))=1 according to the formula, and then calculate k[k_1;k_2]=[3;1]. From this, the D2 and E2 points can be calculated as shown in the figure. Compare the key values and choose the smallest one, which is D2. The g value of D2 is updated to 1 according to the formula min_s(c(s’,s)+g(s’)=0+1=1, and then the calculation is continued.
In the second step, step2, you need to take D2 as the center to calculate C1, C2, C3, D1, D2, D3, E1, E2, and E3. According to the calculation method of step1 in the first step, the values are calculated as shown in the figure. Among them, the key of D3 is [3;1] the smallest (optimal), so D3 is selected as the further extension point.
In the third step, step3, you need to take D3 as the center to calculate C2, C3, D2, D3, E2, and E3. The calculation of each value is shown in the figure, where the key of C1 is [3;2] the smallest (optimal), so C1 is selected as the further expansion point.
In the fourth step, step4, you need to take C1 as the center and perform calculations on B1, B2, C2, D1, and D2. The calculation of each value is shown in the figure, where the key of B1 is [3;3] the smallest (optimal), so B1 is selected as the further expansion point.
In the fifth step, step5, you need to calculate A1, A2, B2, C1, and C2 with B1 as the center. The calculation of each value is shown in the figure, A1 is the starting point, and the algorithm ends.
So the path is A1→B1→C1→D2→E3
When the map changes
When a point D2 in the map becomes an obstacle, the starting node becomes B1, the position is C1, the target point is still E3, and the heuristic value h becomes the following figure: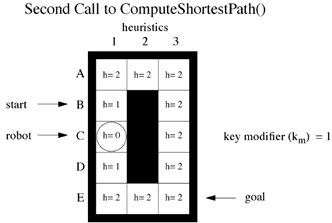
At this time, k_m=k_m+h(s_last,s_start)=0+1=1, change the heuristic value h of each point. The D*Lite algorithm is updated as shown below.
The first is to calculate the cost of change, that is, the Edge Cost Changes step. The change is C1. It is based on the calculation formula rhs(s)=min_s Succ(s)(c(s’,s)+g(s’)=1+3=4. At this time, g(s) is less than rhs(s), which is inconsistent , That is, encounter obstacles, g(u)=∞, update all predecessor nodes (line 19-20 of the algorithm). Therefore, start from step1 and re-search according to the previous path, but there is no need to calculate too many other nodes at this time Grid. So, go back to E2 and start searching (step1), then search at D1 (step2), then search at C1, and then reach the current robot position and terminate the search.
Therefore, the updated path is C1→D1→E2→E3.
